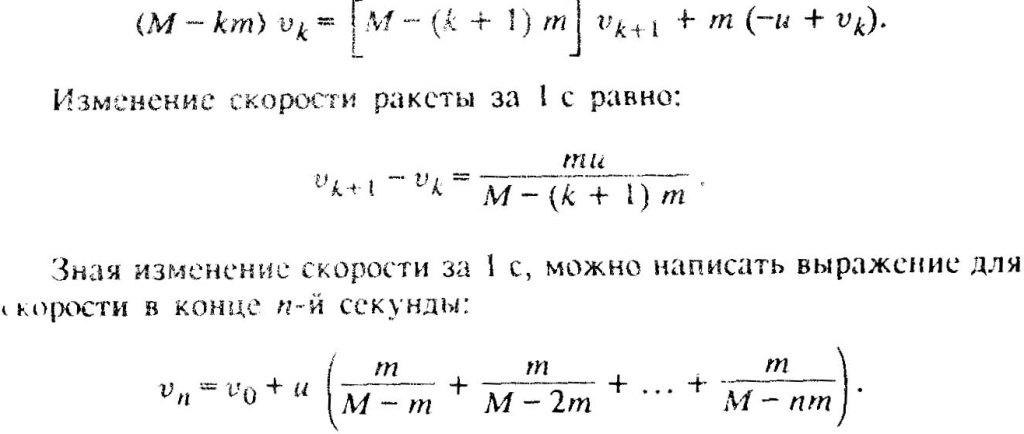Примеры решения задач
Закон сохранения импульса целесообразно применять для решения тех задач, в которых требуется определять скорости, а не силы или ускорения. Конечно, решать подобные задачи можно, используя законы Ньютона. Но применение закона сохранения импульса упрощает решение.
Прежде чем решать задачу с помощью закона сохранения импульса, надо выяснить, можно ли его применить в данном случае. Закон можно применять для замкнутой системы или же в случае, когда сумма проекций сил на какое-либо направление равна нулю, а также когда импульсом внешних сил можно пренебречь.
Для решения задачи нужно записать закон в векторной форме.
После этого векторное уравнение записывают в проекциях на оси выбранной системы координат. Выбор направления осей диктуется удобством решения задачи. Если, например, все тела движутся вдоль одной прямой, то координатную ось целесообразно направить вдоль этой прямой.
При решении некоторых задач приходится использовать дополнительно уравнения кинематики.
Некоторые задачи решаются с применением уравнения для изменения импульса в форме.
(Задача 1)
Стальной шарик массой 0,05 кг падает с высоты 5 м на стальную плиту. После столкновения шарик отскакивает от плиты с такой же по модулю скоростью. Найдите силу, действующую на плиту при ударе, считая ее постоянной. Время соударения равно 0,01 с.
Решение
При ударе шар и плита действуют друг на друга с силами, равными по модулю, но противоположными по направлению. Определив силу, действующую на шарик со стороны плиты, мы тем самым найдем силу, с которой шарик действовал на плиту за время /\t течение которого длится соударение.
Во время соударения на шарик действуют две силы: сила тяжести mg и сила F со стороны плиты.
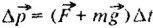
Обозначим через V1 скорость шарика непосредственно до удара о плиту, а через V2 скорость после удара, тогда изменение импульса шарика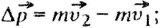 
поэтому
поэтому В проекциях на ось Y это уравнение запишется так:
mV1 – (-mV1) = (F – mg)/\t
Учитывая, что V2 = V1 = V, получим
F = mg + (2mv//\t)
Модуль скорости шарика при падении его с высоты h определяется по формуле V = V2gh = 10 м/с. Теперь, используя выражение, найдем модуль F:
F = 0,5H + 100H = 100,5H
По третьему закону Ньютона
F1= - F
Следовательно, F1 = 100,5H; эта сила приложена к плите и направлена вниз. Заметим, что, чем меньше время взаимодействия /\t, тем большим будет значение величины (2mv//\t) в формуле по сравнению с mg.
Поэтому при соударении можно не учитывать силу тяжести. Если бы шар был сделан из пластилина, то он прилип бы к плите и модуль изменения его импульса был бы в 2 раза меньше. Соответственно и сила, действующая на плиту, была бы также в 2 раза меньше.
(Задача 2)
Во время маневров на железнодорожной станции две платформы массами m1 = 2,4*104 кг и m2 = 1,6*104 кг двигались навстречу друг другу со скоростями, модули которых равны v1 = 0,5 м/c и v2 = 1 м/с. Найдите скорость их совместного движения после того, как сработала автосцепка?
Решение
Изобразим схематично движущиеся платформы до столкновения. Внешние силы N1 и m1g, N2 и m2g, действующие на тела системы, взаимно уравновешены. На платформы действуют еще силы трения, которые являются внешними для системы. При качении платформ по рельсам силы трения невелики, поэтому за малый интервал времени столкновения они заметно не изменяют импульс системы. Следовательно, можно применить закон сохранения импульса:
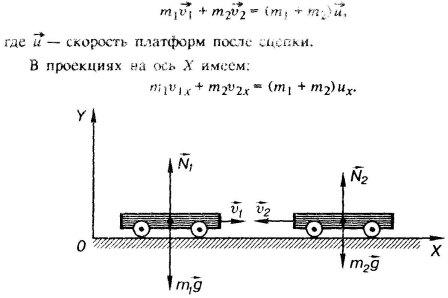
Так как V1x = V1, а V2x = -V2, то
U = (m1V1 – m2V2)/(m1 + m2) = - 0,1 м/c
Отрицательный знак проекции скорости показывает, что скорость направлена противоположно оси X (справа налево).
(Задача 3)
Два пластилиновых шарика, отношение масс которых m2/m1 =4, после соударения слиплись и стали двигаться по гладкой горизонтальной поверхности со скоростью U. Определите скорость легкого шара до соударения, если он двигался втрое быстрее тяжелого (V1=3V2), а направления движения шаров были взаимно перпендикулярны. Трением пренебречь.
Решение
Так как скорости V1 и V2 шаров взаимно перпендикулярны, то оси прямоугольной системы координат удобно направить параллельно скоростям. Согласно закону сохранения импульса имеем:
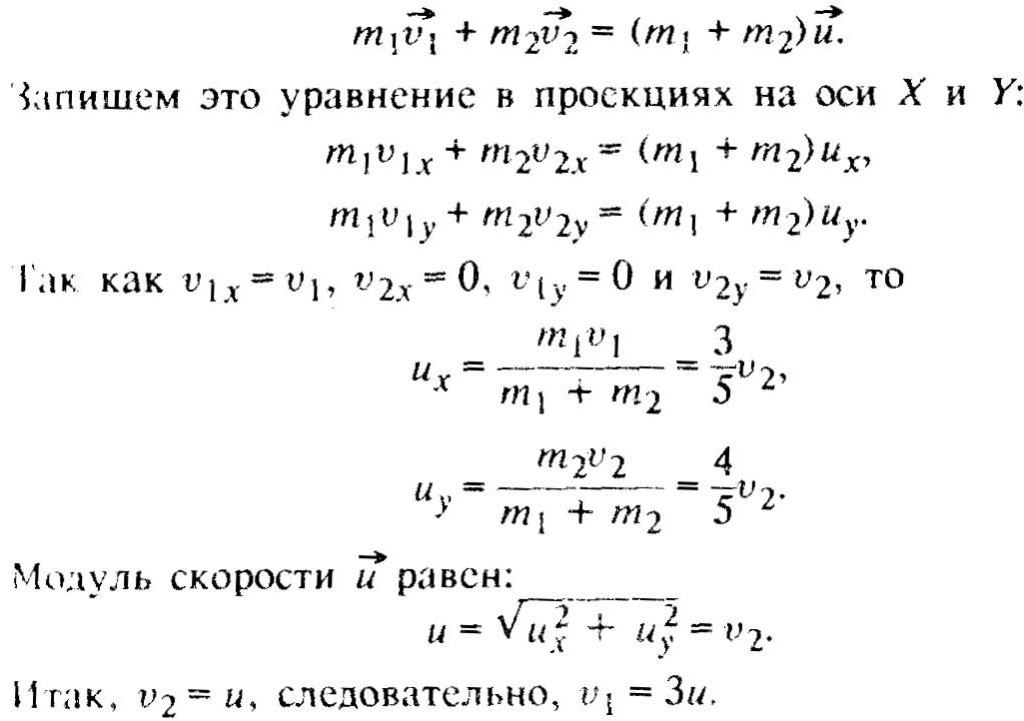
(Задача 4)
Кузнечик сидит на конце соломинки длиной l, которая лежит на гладком полу. Кузнечик прыгает и попадает на другой конец соломинки. С какой минимальной начальной скоростью относительно земли Vmin он должен прыгнуть, если его масса M, а масса соломинки m? Сопротивление воздуха и трение не учитывать.
Решение
Направим ось Y вверх, а ось X вдоль соломинки по направлению прыжка кузнечика. Проекции скорости V кузнечика на координатные оси соответственно равны:
Vx = Vcosa и Vy = Vsina.
Рассмотрим систему кузнечик-соломинка. На тела системы внешние силы действуют лишь по вертикальному направлению (трение отсутствует).
Так как сумма проекций внешних сил на ось равна X равна 0, то сохраняется сумма проекций импульсов кузнечика и соломинки на ось X:
MVx +mV1x = 0 или MVcosa + mV1x = 0
Где V1x – проекция скорости соломинки относительно пола.
Отсюда
V1x = -(MVcosa)/m
Знак минус указывает, что соломинка получает скорость V1, направленную противоположно оси X.
Далее задача решается с помощью формул кинематики
Очевидно, что модуль скорости кузнечика минимален тогда, когда максимален знаменатель дроби полученного выражения. Как известно, значение синуса не может быть больше 1. Итак,
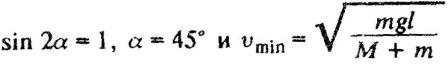
(Задача 5)
В начальный момент ракета массой M имела скорость V0. В конце каждой секунды из ракеты выбрасывается порция газа массой m. Скорость порции газа отличается от скорости ракеты до сгорания данной массы газа на постоянное значение, равное u, т.е. скорость истечения газа постоянна. Определите скорость ракеты через n секунд. Действие силы тяжести не учитывать.
Решение
Обозначим через Vk скорость ракеты в конце k-й секунды. В конце (k+1)-й секунды из ракеты выбрасывается газ массой m, который уносит с собой импульс, равный m(-u+Vk). Из закона сохранения импульса, записанного для модулей векторов, следует, что
